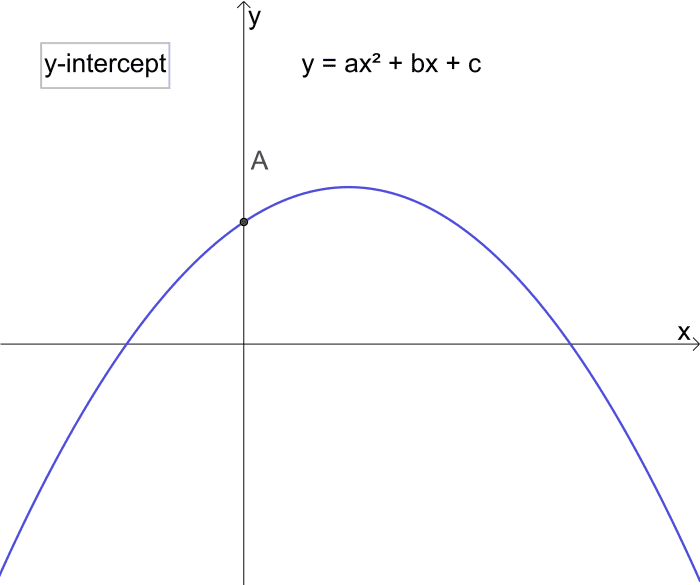
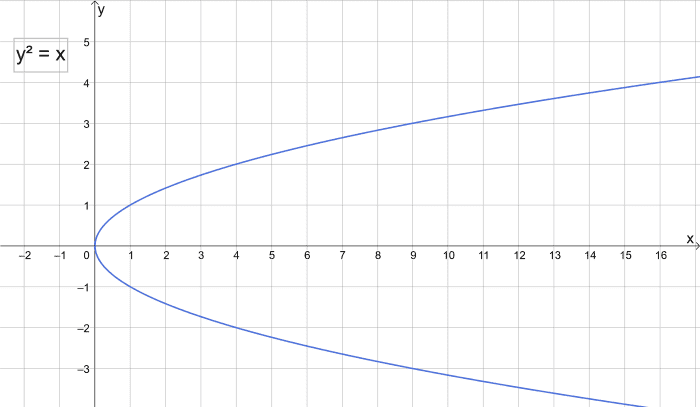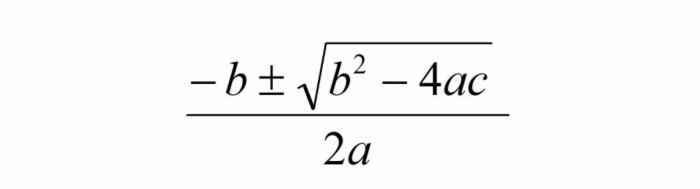抛物线方程与图，准线与焦点，如何求二次方程的根

抛物线，一个数学函数

在本教程中，您将学习一个称为抛物线的数学函数。我们将首先介绍抛物线的定义以及它与称为锥的实体形状的关系。接下来，我们将探索抛物线方程的不同表达方式。还将介绍如何计算出抛物线的极大值和最小值，以及如何找到与x和y轴的交点。最后，我们将发现什么是二次方程以及如何求解它。

抛物线的定义

“一个轨迹是由满足特定方程的所有点组成的曲线或其他图形。

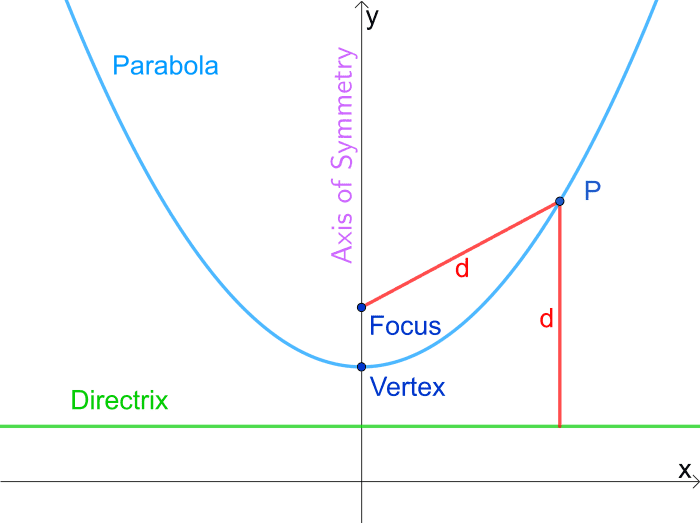
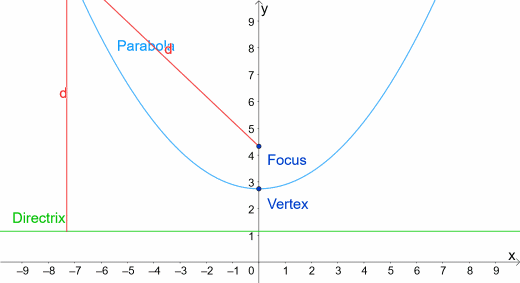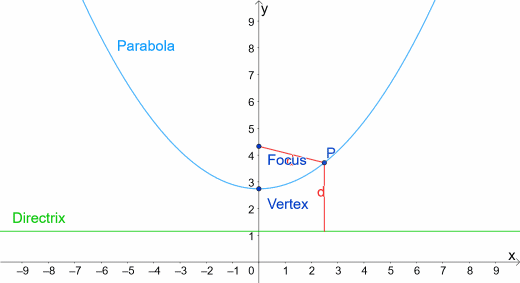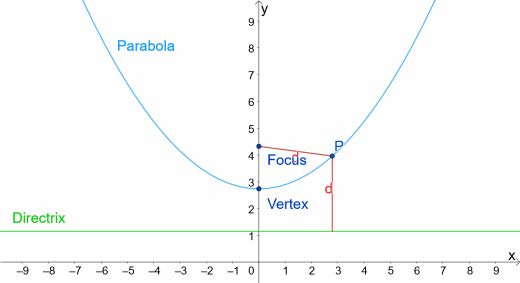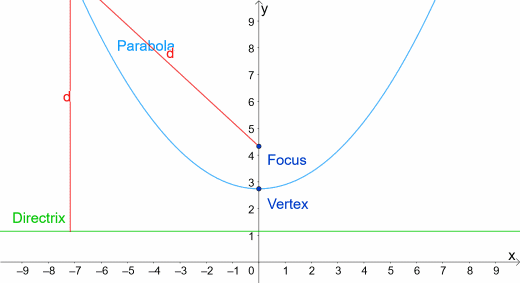
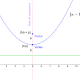
我们定义抛物线的一种方法是它是两点的轨迹这些点到这条线的距离相等准线一个点叫做的焦点。所以抛物线上的每个点P到焦点的距离都与到准线的距离相同，就像你在下面的动画中看到的那样。

我们还注意到，当x = 0时，从P到焦点的距离等于从顶点到准线的距离。焦点和准线到顶点的距离相等。

抛物线是一个圆锥曲线

另一种定义抛物线的方法

当一个平面与一个圆锥相交时，我们会得到不同的形状圆锥部分平面与圆锥体外表面相交的地方。如果平面平行于圆锥的底部，我们画一个圆．随着下面动画中的角度A的变化，它最终会变成等于B，而圆锥截面是一条抛物线。

抛物线方程

我们有几种表达抛物线方程的方法:

• 作为二次函数
• 顶点的形式
• 关注形式

我们稍后会探讨这些，但首先，让我们看看最简单的抛物线。

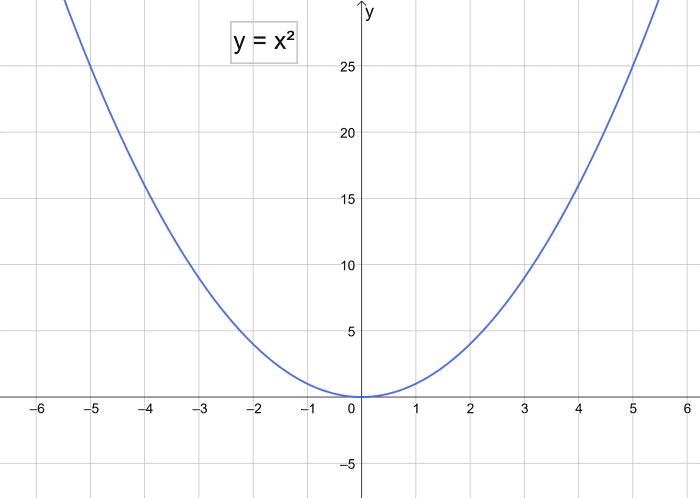
最简单抛物线y = x²

^{顶点在原点(0,0)的最简单抛物线方程为y = x²。}

^{y的值就是x的值乘以它自己。}

给x一个系数!

最简单的抛物线是y = x²，但如果我们给x一个系数，我们可以生成无限条不同“宽度”的抛物线，这取决于系数ɑ的值。

令y =ɑx²

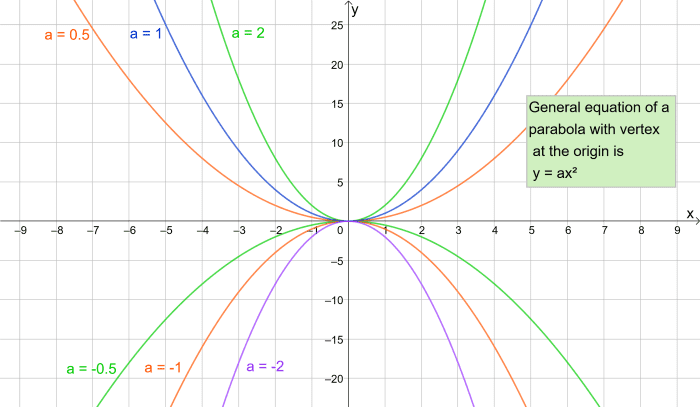
在下面的图表中，ɑ有不同的值。注意，当ɑ为负时，抛物线是“颠倒的”。稍后我们将进一步了解这一点。记住y =ɑx²抛物线方程的形式是顶点在原点处。

使ɑ变小会产生“更宽”的抛物线。如果我们让ɑ变大，抛物线就会变窄。

把最简单的抛物线转向它的一边

如果我们转动抛物线y = x²在它这边，我们得到一个新函数y²= x或x = y²．这意味着我们可以把y看成自变量，平方它就得到x的对应值。

所以:

当y = 2时，x = y²= 4

当y = 3, x = y²= 9

当y = 4时，x = y²= 16

等等……

就像垂直抛物线的情况一样，我们可以再给y加一个系数^2.

我们有x =ɑy²

平行于Y轴的抛物线的顶点形式

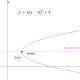
我们表达抛物线方程的一种方法是用顶点的坐标表示。方程取决于抛物线的轴是平行于x轴还是y轴，但在这两种情况下，顶点都位于坐标(h,k)。在方程中，ɑ是一个系数，可以有任何值。

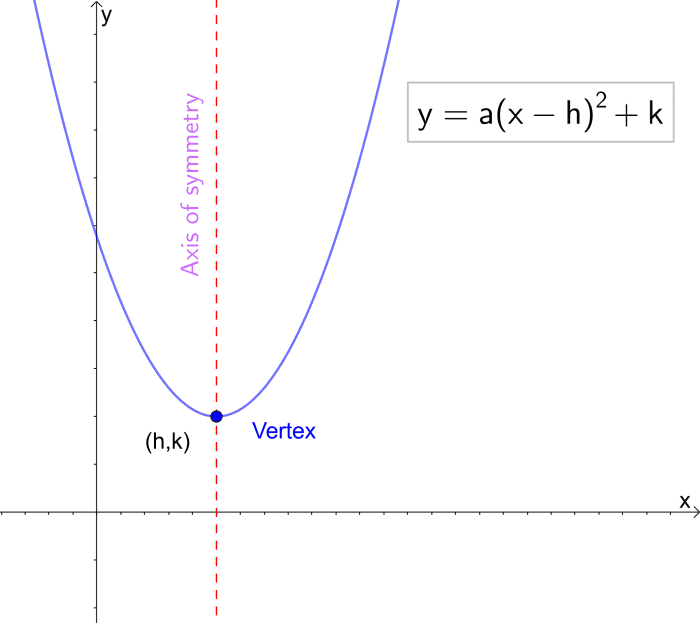
当轴与y轴平行时:

Y =ɑ(x - h)²+ k

如果ɑ= 1并且(h,k)是原点(0,0)，我们就得到了我们在教程开始时看到的简单抛物线:

Y = 1(x - 0)²+ 0 = x²

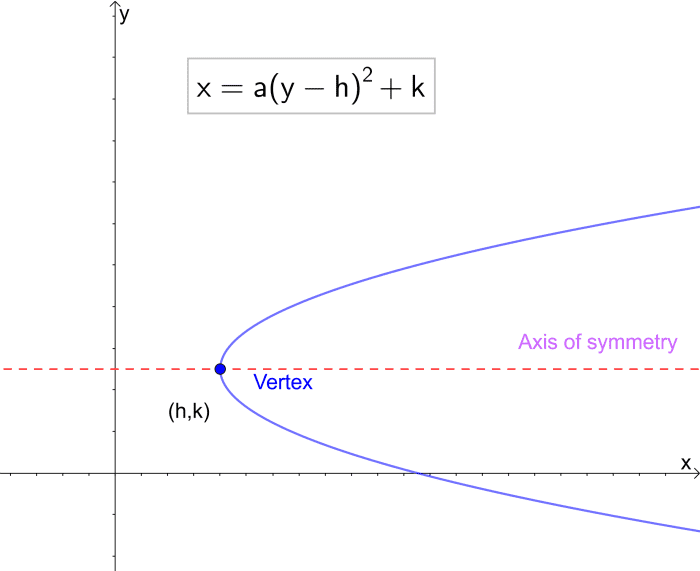
当轴与x轴平行时:

X =ɑ(y - h)²+ k

注意，这并没有给我们任何关于焦点或准线位置的信息。

用焦点坐标表示的抛物线方程

另一种表示抛物线方程的方法是用顶点(h,k)和焦点的坐标表示。

我们看到:

Y =ɑ(x - h)²+ k

利用毕达哥拉斯定理，我们可以证明系数ɑ= 1/4p，其中p是焦点到顶点的距离。

当对称轴平行于y轴时:

将ɑ= 1/4p替换为:

Y =ɑ(x - h)²+ k = 1/(4p)(x - h)²+ k

方程两边同时乘以4p:

4py = (x - h)²+ 4 pk

重新安排:

4p(y - k) = (x - h)²

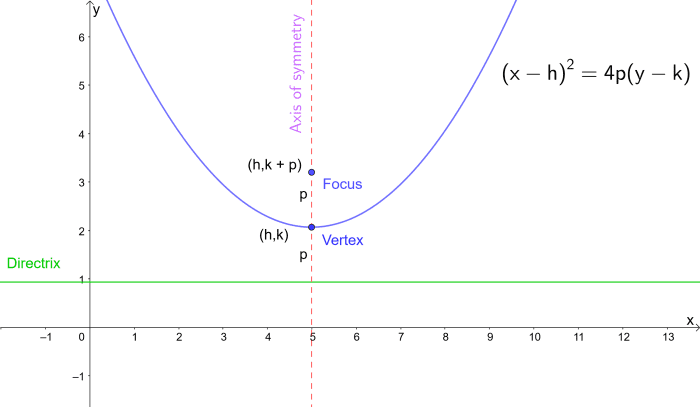
或

(x - h)²= 4p(y - k)

类似的:

当对称轴平行于x轴时:

类似的推导可以得到:

(y - k)²= 4p(x - h)

例子:

求最简单抛物线y = x的焦点²

答:

由于抛物线平行于y轴，我们使用上面学过的方程:

(x - h)²= 4p(y - k)

首先，找到顶点，即抛物线与y轴的交点(对于这个简单的抛物线，我们知道顶点在x = 0处)

令x = 0，令y = x²= 0²= 0

因此，顶点在(0,0)处

但顶点是(h,k)因此h = 0 k = 0

将h和k的值代入方程(x - h)²= 4p(y - k)化简为

(x - 0)²= 4p(y - 0)

给我们

x²= 4 py

现在把这个和抛物线y = x的原始方程比较一下²

我们可以把它写成x²= y，但y的系数是1，所以4p一定等于1,p = 1/4。

从上图中，我们知道焦点的坐标是(h, k + p)，所以将我们算出的h, k和p的值代入，我们得到顶点的坐标为

(0,0 + 1/4)或(0,1 /4)

二次函数是抛物线

考虑函数y =ɑx²+ bx + c

这叫做二次函数因为x变量的平方。

这是另一种表示抛物线方程的方法。

如何确定抛物线打开的方向

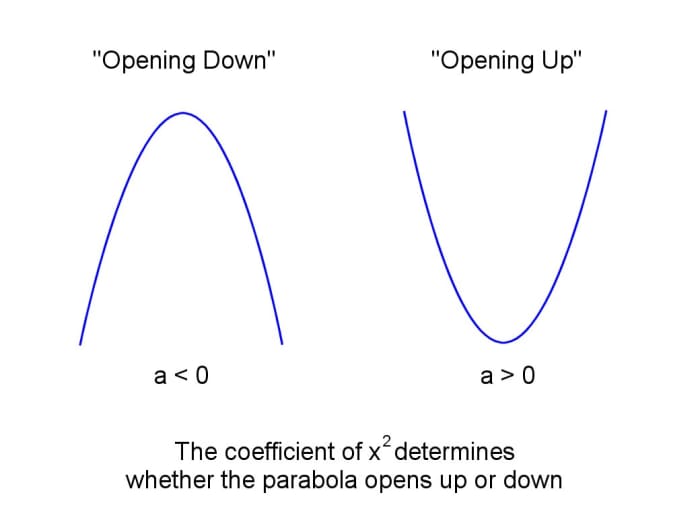
不管用哪种形式的方程来描述抛物线，x的系数²决定抛物线是“向上”还是“向下”。打开意味着抛物线有一个最小值，y的值在最小值两边都增加。向下开放意味着它会有一个最大值，y的值在最大值两边都是减小的。

• 如果ɑ是正的，抛物线就会打开
• 如果ɑ为负，抛物线将向下打开

如何求抛物线的顶点

从简单的微积分我们可以推导出抛物线的最大值或最小值出现在x = -b/2ɑ

将x代入方程y =ɑx²+ bx + c得到对应的y值

y =ɑx²+ bx + c

=ɑ(ɑ- b / 2)²+ b(-b/2ɑ

=ɑ(b²/ 4ɑ²) - b²/2ɑ+ c

收集b²条款和重新安排

= b²(1/4ɑ- 1/2ɑ

= - b²/4ɑ+ c

= c -b²/ 4

最后，最大值或最小值出现在点(-b/2ɑ，c -b²/ 4ɑ)

例子:

求方程y = 5x的顶点²- 10x + 7

1. 系数a是正的，所以抛物线是开口的，顶点是最小值
2. ɑ= 5,b = -10, c = 7，所以最小值的x值出现在x = -b/2ɑ= - (-10)/(2(5))= 1
3. 最小值的y值在c - b处²/ 4。将a b c代入，得到y = 7 - (-10)²/ (4(5)) = 7 - 100/20 = 7 - 5 = 2

顶点在(1,2)处

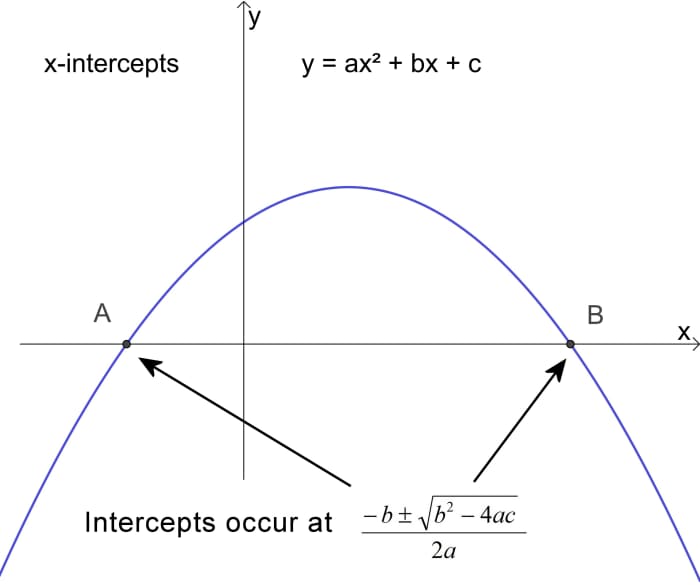
如何求抛物线的x截距

一个二次函数y =ɑx²+ bx + c是抛物线的方程。

如果把二次函数设为0，就得到a二次方程

例如ɑx²+ bx + c = 0．

从图形上看，使函数等于0意味着设置函数的条件，使y值为0，换句话说，在抛物线与x轴截距的地方。

二次方程的解可以求出这两点。如果没有实数解，即解是虚数，抛物线就不与x轴相交。

解决方案根二次方程的，由方程给出:

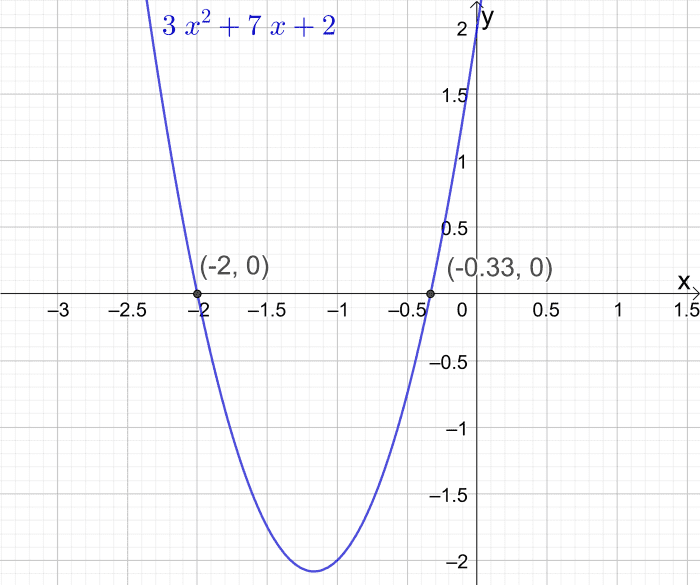
例1:求抛物线y = 3x的x轴截距²+ 7x + 2

解决方案

• Y =ɑx²+ bx + c

• 在这个例子中，y = 3x²+ 7x + 2

• 确定系数和常数c

• ɑ= 3,b = 7, c = 2

• 二次方程3x的根²+ 7x + 2 = 0在x = (-b±√(b)处²- 4ɑc)) / 2ɑ

• 代替ɑ，b和c

• 第一个根在x =(-7 +√(7)处²- 4 × 3 × 2)) / (2 × 3) = -1/3

• 第二个根是(-7 -√(7)²- 4 × 3 × 2)) / (2 × 3) = -2

• x轴在(- 2,0)和(-1/ 3,0)处截距

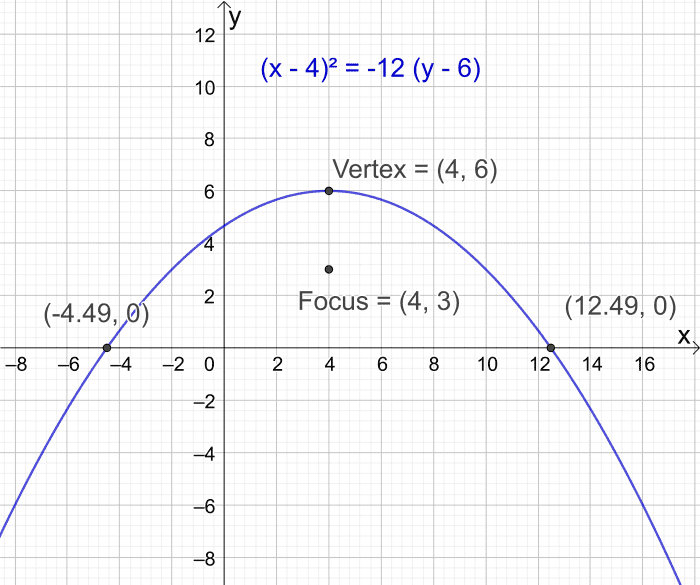
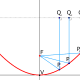
例2:求顶点位于(4,6)并聚焦于(4,3)的抛物线的x轴截距

解决方案

• 焦点顶点形式的抛物线方程为(x - h)²= 4p(y - k)
• 顶点是(h,k) h = 4 k = 6
• 焦点位于(h, k + p)，在这个例子中，焦点位于(4,3)，所以k + p = 3。但是k = 6，所以p = 3 - 6 = -3
• 代入方程(x - h)²= 4p(y - k) so (x - 4)²= 4(-3)(y - 6)
• 简化给予(x - 4)²= -12(y - 6)
• 把方程展开得到x²- 8x + 16 = -12y + 72
• 重新排列12y = -x²+ 8x + 56
• 令y = -1/12x²+ 2/3x + 14/3

• 系数a = -1/12, b = 2/3, c = 14/3

• 根在(-2/3±√((2/3))²- 4 (-1/12) (14/3))) / (2 (-1/12)

• 这就得到x = -4.49和x = 12.49
• x轴截距为(-4.49,0)和(12.49,0)

如何求抛物线的y轴截距

为了求出抛物线的y轴截距(y截距)，我们设x为0，并计算y的值。

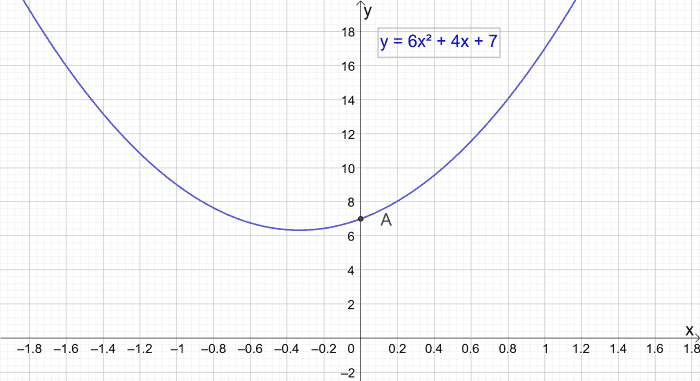
例3:求抛物线y = 6x的y轴截距²+ 4x + 7

解决方案:

Y = 6x²+ 4x + 7

设x为0

Y = 6(0)²+ 4(0) + 7 = 7

截距在(0,7)处

抛物线方程摘要

抛物线在现实世界中是如何使用的

抛物线不仅仅局限于数学。抛物线形状在自然界中出现，我们在科学技术中使用它是因为它的性质。

• 当你把球踢向空中或发射炮弹时，其轨迹是抛物线
• 汽车前灯或手电筒的反光镜是抛物线形的
• 反射式望远镜的镜子是抛物面的
• 卫星天线呈抛物线形状，雷达天线也是如此
• 用来听微弱声音的麦克风可以安装抛物面反射器来收集声音。麦克风位于焦点处，用于收集声音。

对于雷达天线、卫星天线、无线电和光学望远镜，抛物线的特性之一是平行于其轴的一束电磁辐射将被反射向焦点。相反，在车头灯或手电筒的情况下，来自焦点的光将被反射器反射，并以平行光束向外传播。

相关阅读:弹丸运动方程的推导

确认

所有图形都是使用GeoGebra Classic创建的。

©2019尤金·布伦南

评论

Srinjan Sanyal2020年5月27日:

内容非常好。

rafia2019年9月29日，巴基斯坦拉合尔:

嘿，你是个好老师!我以前不知道向上或向下的图形。但现在我知道了。谢谢你！