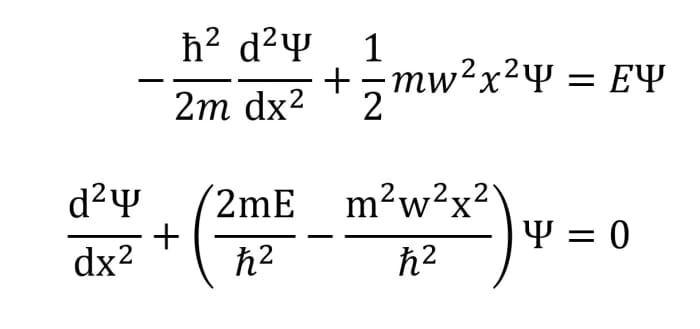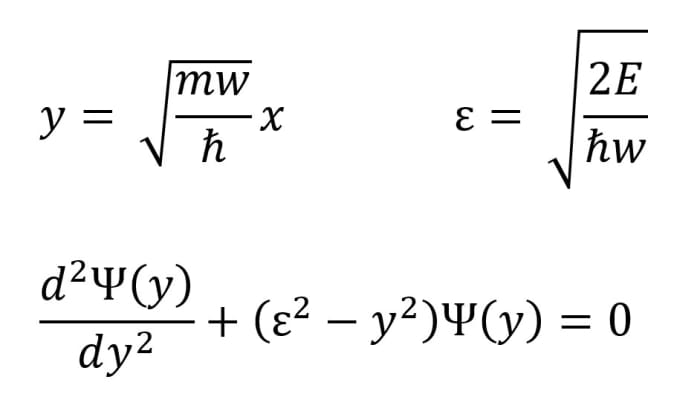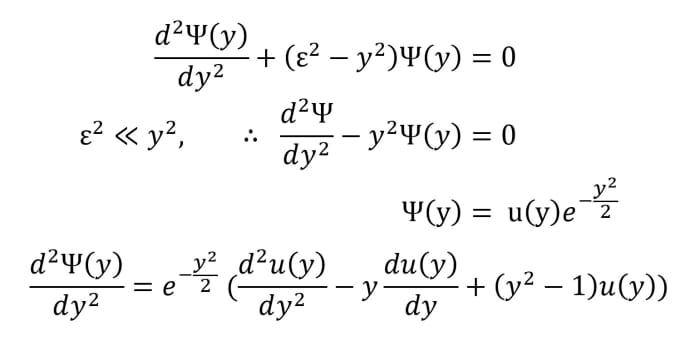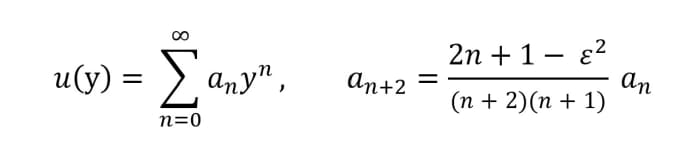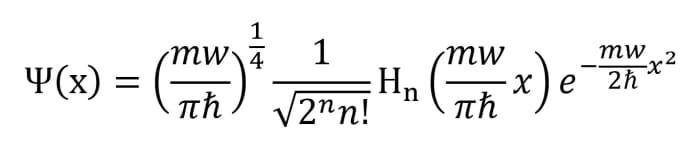简单谐振子Schrödinger方程的解

Mohammad Yasir是德里大学物理学毕业生，目前在印度理工学院攻读硕士课程。

提出问题

简谐振子是理解量子力学和Schrödinger方程概念的一个极好的研究。它也是一种奇妙的方式，可以看到量子领域变成经典力学的世界，当我们进入越来越高的能量状态时，从而增加n的值。

首先，回忆SHM是由运动方程所描述的F = -kx．这对应于势能V =½kx²．比例常数的值由K = mw²．这为我们提供了建立Schrödinger方程所需的所有工具。

解方程

在我们开始之前，引入变量的微小变化并将常数捆绑在一起会对我们有帮助。

正如你所看到的，这个小小的重新排列显著地清理了我们的方程。现在，我们首先试着解出y趋于无穷时的渐近条件，因此，相对于y²,ε²可以忽略不计。这允许我们假设一个解的形式如下:

ψ(y) = u(y) exp(-y²/ 2)

请注意，包含附加函数u(y)是必要的，因为我们目前讨论的是渐近区域附近的解。u(y)的形式和值将在后面计算。此外，要谨慎地知道Ψ(y)的值不是随机选择的。事实上，这很有道理。来看看:

现在我们得到了Ψ(y)关于y的二阶导数的表达式。如果我们把它代入方程1，我们会发现指数项抵消了，我们只剩下一个关于u(y)的表达式。在继续之前，请自己尝试一下。你应该得到这样一个方程:

d²u / dy²- (2y) du/dy + (ε²- 1) u = 0 ----- (2)

你能猜到我们下一步要做什么吗?这个方程看起来很简单，但它没有直接解。相反，我们将利用幂级数方法得到u(y)的表达式。我就不详细讲了，因为你一定已经学过了。如果没有，我建议你通过这它解释了所有你可能需要知道的关于幂级数和求解二阶线性ode的知识。

现在我们将跳到u(y)的递归关系，将其幂级数形式表达式代入方程2后得到。

看幂级数

对于n非常大的值，两个连续项的比值接近于值2/n，这比ψ(y)初始解中的指数衰减项发散得快得多。因此，为了波函数具有任何物理意义，这个级数必须终止。

要做到这一点，指数为n+2的系数必须在n的某一特定值处消失，设为j。

因此，我们有了n的最大可能值的表达式，用j表示，并由2j + 1 = ε给出²

在进一步讨论之前，回忆一下ε与谐振子的能量有关，上面的方程只是给了我们一个E的表达式_n．

E_n= (n +½)ħw

这将我们引向另一个革命性的概念。

波函数呢?

如果你回顾一下，我们已经在技术上解决了薛定谔方程。我们知道u(y)的幂级数形式的递归关系，我们已经知道完整的解是Ψ(y) = u(y) exp(-y)²/ 2)。剩下的就是将这个波函数归一化，并替换我们改变过的所有变量。一旦你这样做了，你会得到一个这样的表达式:

函数H_n(x)就是所谓的Hermite多项式。我鼓励你们更多地了解它们，因为你们会在各种物理情况下遇到这些多项式。

量子隧穿

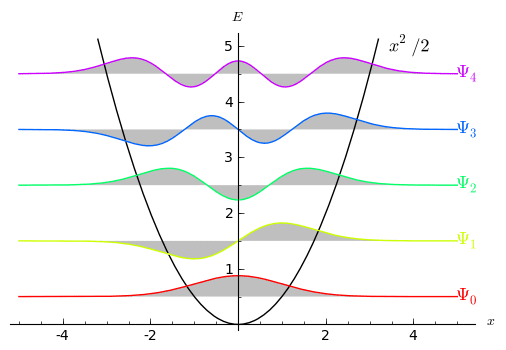
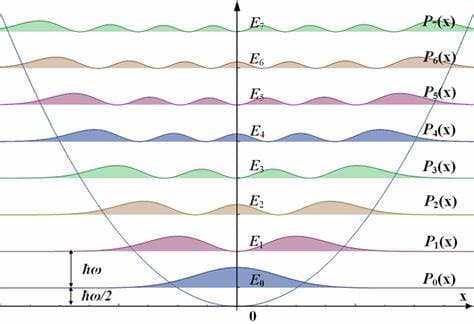
本文开头所附的图像显示了简单谐振子的前几个状态的解的形式。注意，你可以将Ψ与复共轭Ψ相乘^＊来获得在x点找到振子的概率的表达式。虽然我不会详细讨论它，但你可以看到，波函数不会消失在由势曲线给出的经典允许区域之外。相反，它会衰变。你能猜到这是怎么发生的吗?

能量量化到底意味着什么?

经典地说，谐振子的能量由E =½兆瓦²一个²，其中a为振荡幅度。很明显，这可以取任何正值。另一方面，量子振子能量的表达式被下标并由，E_n= (n +½)ħw．这导致了两个认识:

1. 量子振荡器只能存在于州，每一种状态的特征都是能量的半整数倍ħw．除了这些以外的任何能量值量化不允许使用值。
2. 量子振子的基态能量不为零，而经典振子的基态能量为零。

结论

这是关于量子振荡器问题的基本讨论。通过将电子看作耦合谐振子，利用这个概念来解释金属的电子性质。这一现象还有其他各种应用。

如果你是一名大学生，我建议你跟随这个链接其中几个解决了谐振子的问题。此外，得到一个绘图软件，并尝试绘制n = 10的波函数。当n = 100时再试一次。比较你得到的曲线与经典概率密度．你能从中得出什么结论?

据作者所知，这些内容是准确和真实的，并不意味着要取代来自合格专业人士的正式和个性化的建议。

©2022穆罕默德·亚西尔