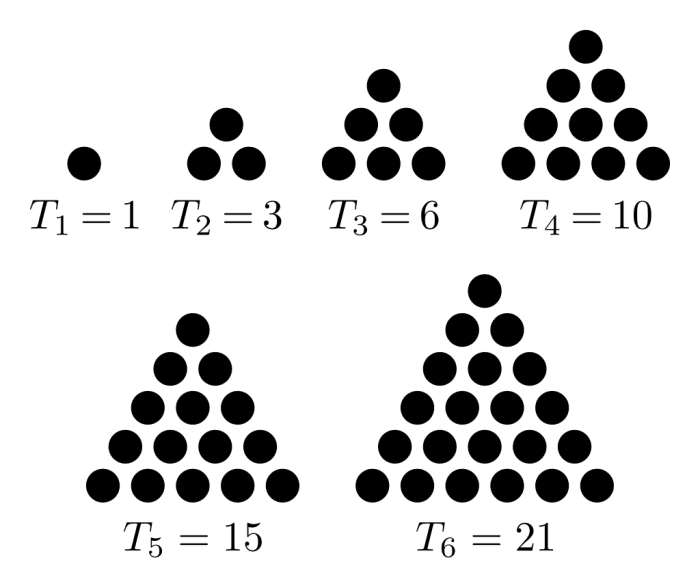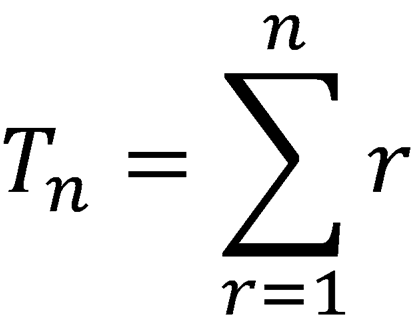什么是三角数?

我以前是一名数学老师，也是DoingMaths的老板。我喜欢写关于数学、数学应用和有趣的数学事实的文章。

什么是三角数?

三角数是将圆点排列成越来越大的等边三角形而形成的数字序列。从下图中可以看出，第一个三角形数1是由一个点组成的。

为了得到第二个三角形数3，我们在原来的点下面加上另一行，这次包含两个点。

然后我们加一行三个点，得到第三个三角形数6。

我们继续这样做，每次在三角形的底部添加一个额外的行，它比前一行多包含一个点。这给出了序列1,3,6,10,15,21，等等。

三角数的代数描述

我们已经看到了如何用图示的方法构造三角数序列，但现在让我们试着用数学形式表示它。从我们到目前为止所做的可以看出，一个三角数与下一个三角数之间的差值每次都增加1。

如果我们用T表示第一个三角数₁，第二个为T₂，以此类推，使n^th三角数是T_n，并进一步定义第0个三角数为0，得到:

T₀= 0

T₁= T₀+ 1 = 1

T₂= T₁+ 2 = 3

T_3.= T₂+ 3 = 6

T₄= T_3.+ 4 = 10

等等。

因此，我们得到，任何三角数都是所有正整数的和，直到并包括它的项数，即T_n= 1 + 2 + 3 + 4 +…+ n。

在求和法中，这可以表示为如下图所示。

如何计算第n个三角数

我们知道T_n= 1 + 2 + 3 +…

如果我们重写T_n但是反过来求和，我们得到T_n= n + n−1 + n−2 +…+ 2 + 1

把这两行加起来，我们得到:

T_n+ T_n= (n + 1) + n (n−1 + 2)+(−2 + 3 ) + ... + ( n + 1)

2 t_n= (n + 1) + (n + 1) + (n + 1) +…

由于这个级数中有n项，我们得到:

2 t_n= n × (n + 1)

T_n= n × (n + 1) / 2

用这个公式，我们可以很快地计算出级数中的任何项。

例如T₅₀= 50 × 51 / 2 = 1275

T₁₀₀₀= 1000 × 1001 / 2 = 500

三角数与平方数之间的联系

也许令人惊讶的是，三角形数和平方数之间有一个非常简单的联系。首先让我们想象一下。

如果我们将三角形对齐到一边，创建直角三角形而不是等边三角形，然后我们可以取两个连续的三角形，将其中一个旋转180°，将它们放在一起形成一个正方形。这可以在下面的图片中看到，我们已经取了第三个三角形数(红色)和第四个三角形数(蓝色)。把它们加在一起，我们得到一个大小为4 × 4 = 16的正方形。

三角数和平方数:代数

我们可以很容易地看到，这个方法可以应用到我们迄今为止见过的所有三角形数，如果我们将任何连续的三角形数相加，我们确实得到一个平方数。

例如;1 + 3 = 4,3 + 6 = 9,6 + 10 = 16。

此外，我们可以看到，到目前为止，我们得到了所有的平方数1(等于第一个三角数)，4,9,16，等等，没有跳过任何一个。

这可以通过考虑我们之前创建的公式来代数表示。

T_n+ T_n−1= n × (n + 1) / 2 + (n−1)× n / 2

= (n²+ n) / 2 + (n)²−n) / 2

n = 2²/ 2

= n²

因此，我们已经证明，任何连续的三角形数必须相加才能得到一个平方数和任何平方数n²可以由T_n和T_n−1．

三角数与立方数之间的联系——尼可马库斯定理

三角形数和立方数之间也有一个令人惊讶的简单联系。n的平方^th三角数等于前n个立方数的和。

在代数上，这可以表示为:

T_n²(1 + 2 + 3 +…+ n)²= 1^3.+ 2^3.+ 3^3.+形容词+名词^3.．

这就是著名的尼哥马库斯定理，以古希腊数学家尼哥马库斯的名字命名。

三角数的实际应用

也许三角数最著名的应用是在握手问题中。如果房间里有n个人，需要握几次手才能让每个人都和其他人握过一次手?

如果房间里只有两个人，握手次数为1次。

如果房间里有3个人，那么a和b、c分别握手，接着b和c握手，总共握手3次。

如果房间里有4个人，可以很容易地计算出需要握手6次。

这可以扩展到n个人。如果房间里有n个人，第一个人需要和房间里的所有人握手，以第一个人为主角握手n−1次。第二个人需要和每个人握手，但是我们已经计算了他和第一个人的握手，所以他们还有n - 2个人可以握手。

继续这个逻辑，我们可以看到，对于n个人，将会有(n−1)+ (n−2)+…+ 2 + 1次握手。正如我们已经看到的，这个等于T_n−1．

因此，不管房间里有多少人，握手的次数总是一个三角数。

欲进一步阅读请访问我的文章关于握手问题．

握手问题也相当于计算在每支球队只进行一次比赛的循环赛小组赛阶段需要进行多少场比赛。例如，在一个4支球队的小组中，将有6场比赛。

据作者所知，这些内容是准确和真实的，并不意味着要取代来自合格专业人士的正式和个性化的建议。

©2021大卫